Mathematical Model for the Dynamics of Anthrax in Human and Animal Populations Incorporating Control Measures

Authors

  • Abdulrahman Abubakar
    Adamawa State Polytechnic, Yola
  • Maigari Jingi Bala
    Adamawa State Polytechnic, Yola
  • Ahmed Goni Umar
    Adamawa State Polytechnic, Yola
  • Musa Abdullahi
    Modibbo Adama University, Yola
  • Umar Gidado
    Government Day Senior Secondary School Hammawa Toungo, Yola

Keywords:

Anthrax, Reproduction Number, Vaccination, Stability, Simulations

Abstract

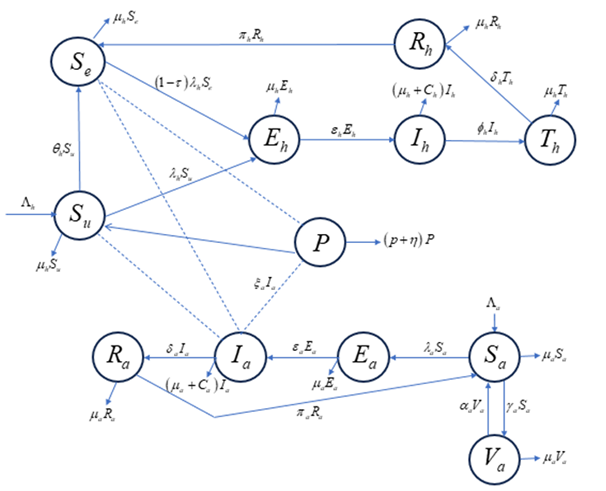
Anthrax is a zoonotic infectious disease caused by the bacterium Bacillus anthracis. In this study, we develop and analyze a deterministic compartmental model, formulated using ordinary differential equations, to explore the transmission dynamics of anthrax between humans and animals. Fundamental properties of the model, such as positivity, boundedness, and the existence of equilibrium points are established, confirming that the model is mathematically and biologically well-posed. The basic reproduction number, ​, is derived using the next-generation matrix approach. Stability analysis shows that the disease-free equilibrium is both locally and globally asymptotically stable when . Additionally, the model possesses a unique endemic equilibrium when , which is also globally stable when . Numerical simulations are conducted to validate and illustrate the theoretical results.

Dimensions

Ahmed, B., Sultan, Y., Fatema, M.S.D., Ara, K., Begun, N., & Mostanzid, S.M. (2010) Anthrax: An emerging zoonotic disease in Bangladesh. Bangladesh Journal of Medical Microbiology, 4:46-50. DOI: https://doi.org/10.3329/bjmm.v4i1.8470

Awoonor-Williams, J.K., Apanga, P.A., Anyawie, M., Abachie, T., Boidoitsiah, & S., Opare, J.L. (2016). Anthrax outbreak investigation among humans and animals in Northern Ghana: Case Report. DOI: https://doi.org/10.9734/IJTDH/2016/22359

Baloba, E.B., & Seidu, B. (2022) A mathematical model of anthrax epidemic with behavioural change. Mathematical modelling and control, 2(4): 253-256. DOI: https://doi.org/10.3934/mmc.2022023

Castillo-Chavez, C., and Song B. (2004). Dynamical model of tuberculosis and their applications, Math. Biosci. Eng., 1 (2), 361-404. DOI: https://doi.org/10.3934/mbe.2004.1.361

Decker, J. (2003) Deadly diseases and epidemics Anthrax. USA: Chelsea House Publishers.

Dragon, D.C., & Rennie, R.P. (1995) The ecology of anthrax spores, Tough but not invincible. The Canadian Veterinary Journal 36: 295–301.

Efraim, J.E., Irunde, J.I., & Kuznetsov, D. (2018). Modeling the transmission dynamics of anthrax disease in cattle and humans. J. Math. Comput. Sci. 8(6): 654-672.

Elijah, B.B., Baba,S. & Christopher, S.B. (2020) Mathematical analysis of the effects of controls on the transmission dynamics of anthrax in both animal and human populations, Computational and Mathematical Methods in Medicine, 1581358. https://doi.org/10.1155/2020/1581358. DOI: https://doi.org/10.1155/2020/1581358

Fasanella, A., Adone R., & Hugh-Jones M. (2016) Classification and management of animal anthrax outbreaks based on the source of infection. Ann Ist Super Sanita 50: 192-195.

Friedman, A., & Yakubu, A. (2013). Anthrax epizootic and migration: persistence or extinction. Mathematical Biosciences. 241(1): 137–144. DOI: https://doi.org/10.1016/j.mbs.2012.10.004

Hahn, B.D., & Furniss, P.R. (1983). “A deterministic model of an anthrax epizootic: threshold results,” Ecological Modelling. 20 (2): 233–241. DOI: https://doi.org/10.1016/0304-3800(83)90009-1

Hethcote, H. W. (2000) The Mathematics of infectious diseases. SIAM Rev. 42: 599–653. https://doi.org/10.1137/S0036144500371907. DOI: https://doi.org/10.1137/S0036144500371907

Nigeria Centre for Disease Control (NCDC), (2023). Anthrax. Viewed June 27, 2023 from http://www.ncdc.gov.ng.

Samad, M.A. (2013). Public health threat caused by zoonotic diseases in Bangladesh. Bangladesh Journal of Veterinary Medicine. 95—120. DOI: https://doi.org/10.3329/bjvm.v9i2.13451

Shaibu, O., Oluwole, D.M. & David, M.T (2018). Mathematical Modelling of the Trans mission Dynamics of Anthrax in Human and Animal Population, Mathematical Theory and Modeling 8(6).

Sinkie, Z.M. & Murthy, S.N., (2016). Modeling and simulation study of anthrax attack on environment. Journal of Multidisciplinary Engineering Science and Technol ogy. 3(4): 4574-4578.

Stoltenow, C.L., (2021). Anthrax. NDSU Extension, USA.

Suma, A.P., Suresh, K.P., Gajendragad, M.R. & Kavya, B. A. (2017). Forecasting an thrax in livestock in Karnataka State using remote sensing and climatic variables. International Journal of Science and Research. 6: 1891–1897.

Van den Driessche, P., and James, W. (2002). Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences, 180, 29-48. DOI: https://doi.org/10.1016/S0025-5564(02)00108-6

Yadeta, W., Giro, A., Amajo, M. & Jilo, K. (2020). Recent understanding of the epi demiology of animal and human anthrax in Ethiopia with emphasis on diagnosis, control and prevention interventions-review. World Jonal of Medical Science. 17: 1-9.

Published

2025-09-15

How to Cite

Abubakar, A., Bala, M. J., Umar, A. G., Abdullahi, M., & Gidado, U. (2025). Mathematical Model for the Dynamics of Anthrax in Human and Animal Populations Incorporating Control Measures. Journal of Science Research and Reviews, 2(3), 166-177. https://doi.org/10.70882/josrar.2025.v2i3.94

Issue

Vol. 2 No. 3 (2025): JOSRAR Vol. 2 No. 3 (May - June)

Section

Articles
Copyright & Licensing

Copyright (c) 2025 Journal of Science Research and Reviews

Creative Commons License

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

  • Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
  • NonCommercial — You may not use the material for commercial purposes.
  • No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits.

How to Cite

Abubakar, A., Bala, M. J., Umar, A. G., Abdullahi, M., & Gidado, U. (2025). Mathematical Model for the Dynamics of Anthrax in Human and Animal Populations Incorporating Control Measures. Journal of Science Research and Reviews, 2(3), 166-177. https://doi.org/10.70882/josrar.2025.v2i3.94

Similar Articles

You may also start an advanced similarity search for this article.