Fractional-Order Mathematical Modeling and Analysis of Malaria Incorporating Control Measures via the Adams–Bashforth–Moulton Method
DOI:
https://doi.org/10.70882/josrar.2026.v3i1.154Keywords:
Malaria, Fractional, Adam-Bashforth-Moulton, Transmission, Control, StrategiesAbstract
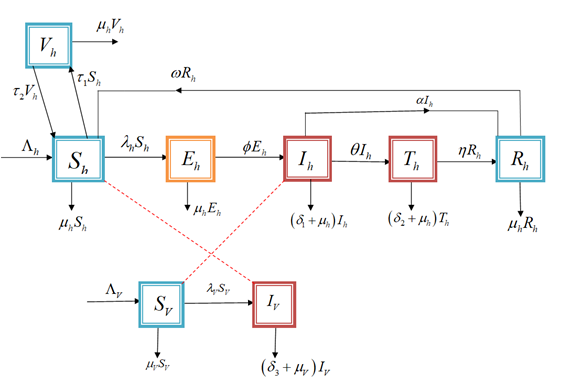
The epidemiological features of malaria infection are taken into consideration in this paper as a fractional-order mathematical model in Caputo derivative. The activities that the model uses to manage the disease are treatment and vaccination to study the effects of the controls on the disease dynamics. The theory of Lyapunov functions determines and verifies the existence and uniqueness of solutions within the frame of the fractional order and the stability of the endemic equilibrium point. The model is numerically obtained with the help of the fractional Adams-Bashforth-Moulton algorithm that will indicate the alteration of the model parameters, and the fractional orders of the model parameters to the impact of each of the mentioned parameters on the course of the disease. It has been established through the application of simulation that the more the disease is treated and vaccinated the less the prevalence of malaria and that the fractional-order models have high level of flexibility and realism than the classical integer order equations. The paper identifies the importance of fractional modeling in the description of the interactions between the effects of memory and nonlocal interaction between the biological systems and this enhances the understanding and control of infectious diseases. The model does however assume that the population is homogeneous mixed and hypothetical values of the parameters thus preventing the empirical validation. To make the model more predictive and practical to use in the formulation of effective control schemes against malaria, then the future research must be capable of addressing the spatial heterogeneity, stochasticity.
References
AbroK., A. Atangana, J.F. Gómez-Aguilar, An analytic study of bioheat transfer Pennes model via modern non-integers differential techniques, Eur. Phys. J. Plus 136 (2021) http://dx.doi.org/10.1140/epjp/s13360-021-02136-x.
Acheneje, G.O., Omale, D., Agbata, B.C., Atokolo, W., Shior, M.M., Bolarinwa, B. (2024), "Approximate solution of the fractional order mathematical model on the transmission dynamics of the co-infection of COVID-19 and Monkeypox using the Laplace-Adomian Decomposition Method," International Journal of Mathematics and Statistics Studies, 12(3), pp. 17–51.
Ahmed, I., Goufo, E.F.D., Yusuf, A., Kumam, P., Chaipanya, P., and Nonlaopon, K. (2021), "An epidemic prediction from analysis of a combined HIV-COVID-19 co-infection model via ABC fractional operator," Alexandria Engineering Journal, 60(3), pp. 2979–2995.
Ali. Z., Zada,. A. Shah K., (2017) Existence and stability analysis of three point boundary value problem, Int. J. Appl. Comput. Math. 3 651–664, http://dx.doi.org/10.1007/s40819-017-0375-8.
Ameh P.O., Omede B.I, and Bolarinwa Bolaji (2020), Dynamical analysis of a two strain treatment model for Anthrax in a population where it is deployed as bio-terrorism weapon. Journal of the Nigerian Society for Mathematical Biology. Volume 3, pp. 34 – 77.
Amos J., Omale D., Atokolo W., Abah E. Omede B.I., Acheneje G.O., Bolaji B. (2024), Fractional mathematical model for the Transmission Dynamics and control of Hepatitis C,FUDMA Journal of Sciences,Vol.8,No.5,pp.451-463, https://doi.org/10.33003/fjs-2024- 0805-2883.
Atokolo, W., Aja, R.O., Aniaku, S.E., Onah, I.S., &Mbah, G.C. (2022), "Approximate solution of the fractional order sterile insect technology model via the Laplace-Adomian Decomposition Method for the spread of Zika virus disease," International Journal of Mathematics and Mathematical Sciences, 2022(1), Article 2297630.
Atokolo, W.A., Remigius Aja, O., Omale, D., Ahman, Q.O., Acheneje, G.O., Amos, J. (2024), "Fractional mathematical model for the transmission dynamics and control of Lassa fever," Franklin open, 2773-1863, https://doi.org/10.1016/j.fraope.2024.100110.
Atokolo, W.A., Remigius Aja, O., Omale, D., Paul, R.V., Amos, J., Ocha, S.O. (2023), "Mathematical modeling of the spread of vector-borne diseases with influence of vertical transmission and preventive strategies," FUDMA Journal of Sciences, Vol. 7, No. 6 (Special Issue), pp. 75–91, https://doi.org/10.33003/fjs-2023-0706-2174.
Bolarinwa Bolaji, Favour Ani, Benjamin Omedea, Godwin Acheneje, Abdullahi Ibrahim (2024). A model for the control of transmission dynamics of human Monkeypox disease in subSaharan Africa. J. Nig. Soc. Phys. Sci. 6 1800. Available online at: https://journal.nsps.org.ng/index.php/jnsps - Scopus indexed Journal.
Bolarinwa Bolaji, U. B. Odionyenma, B. I. Omede, P. B. Ojih, and Abdullahi A. Ibrahim (2023), Modelling the transmission dynamics of Omicron variant of COVID-19 in densely populated city of Lagos in Nigeria, J. Nig. Soc. Phys. Sci. 5 1055. Available online at: https://journal.nsps.org.ng/index.php/jnsps - Scopus indexed Journal.
Chen, Y., Wong, K., & Zhao, L. (2023), "Modeling the impact of vaccination strategies on hepatitis C and COVID-19 coinfection dynamics," Journal of Vaccine, 41(15), pp. 2897–2905.
Chikaki, E., Ishikawa, H. (2009), "A Dengue transmission model in Thailand considering sequential infections with all four serotypes," J. Infect. Dev. Ctries., 3(9), pp. 711–722.
Das, R., Patel, S., & Kumar, A. (2024), "Mathematical modeling of hepatitis C and COVID-19 coinfection in low- and middle-income countries: challenges and opportunities," BMC Public Health, 24(1), pp. 587.
Godwin Acheneje, Daniel Omale, Celestine Agbata, Williams Atokolo, M. Shior and Bolarinwa Bolaji. (2024). Approximate Solution of the Fractional Order Mathematical Model on the Transmission Dynamics on The Co-Infection of COVID-19 and Monkeypox Using the Laplace-Adomian Decomposition Method. International Journal of Mathematics and Statistics Studies, 12 (3), 17-51. https://doi.org/10.37745/ijmss.13/vol12n31751
Godwin Onuche Acheneje, David Omale, William Atokolo and Bolarinwa Bolaji. (2024). Modelling the transmission dynamics of the co-infection of COVID-19 and Monkeypox diseases with optimal control strategies and cost–benefit analysis. Franklin Open 8. 100130. https://doi.org/10.1016/j.fraope.2024.100130 - Elsevier journal (Scopus indexed).
Jalija E., Amos J, Atokolo .W., Omale .D., Abah. E., Alih .U., Bolaji .B. (2025), Numerical investigations on Dengue fever model through singular and non-singular fractional operators. International Journal of Mathematical Analysis and Modelling.
Jalija E., Amos J., Benjamin A., Bolarinwa.B., (2025), fractional order model for HIV/AIDS:Analytical and Generalized fractional Adams-Bashforth-Moulton Approach. Journal of management and Technology.
Nicholas Agahiu, Bolarinwa Bolaji, Godwin Onuche Acheneje and William Atokolo (2024). Approximate solution of fractional order mathematical model on the co-transmission of Zika and Chikungunya virus using Laplace-Adomian decomposition Method. Int. J. Mathematics. 07(03), 47-81.
Odiba Peace, Acheneje Godwin, Bolarinwa Bolaji (2024). A compartmental deterministic epidemiological model with non-linear differential equations for analysing the co-infection dynamics between COVID-19, HIV, and Monkeypox diseases. Healthcare Analytics, 5 100311. Available online at: https://doi.org/10.1016/j.health.2024.100311.
Omale D., Atokolo W., .Akpa. M, (2020) Global stability and sensitivity analysis of transmission dynamics of tuberculosis and its control, A case study of Ika general hospital Ankpa, Kogi State, Nigeria. Acad. J. Stat. Math. 6, 5730-7151.
Omale D., Ojih P., Atokolo. W, Omale A., Bolaji.B. (2021), Mathematical model for transmission dynamics of HIV and Tuberculosis co-infection in Kogi State, Nigeria. Journal of Mathematical Computational Science. 11, No. 5, 5580-5613. Available online at: https://doi.org/10.28919/jmcs/6080.
Omame, A.M., Abbas, M., Onyenegecha, C.P. (2022), "A fractional order model for the cointeraction of COVID-19 and hepatitis B virus," Journal of Mathematical Biology, pp. 112–118.
Omede, B. I., Bolarinwa Bolaji, Olumuyiwa, P. J., Ibrahim, A. A. and Oguntolu F. A (2023). Mathematical analysis on the vertical and horizontal transmission dynamics of HIV and Zika virus co-infection. Franklin open 6 100064. https://doi.org/10.1016/j.fraope.2023.100064. - Elsevier Journal.
Omede, B. I., Olumuyiwa, P. J., Atokolo, W., Bolarinwa Bolaji, and Ayoola, T. A. (2023). A mathematical analysis of the two-strain tuberculosis model dynamics with exogenous reinfection. Healthcare Analytics 4, 100266. https://doi.org/10.1016/j.health.2023.100266 - Scopus indexed Journal.
Omede, B.I., Israel, M., Mustapha, M.K., Amos, J., Atokolo, W., &Oguntolu, F.A. (2024), "Approximate solution to the fractional soil-transmitted helminth infection model using LaplaceAdomian Decomposition Method," International Journal of Mathematics, 07(04), pp. 16–40.
Omonu G. U., Ameh P.O., Omede B.I, and Bolarinwa Bolaji (2019), Mathematical modelling of TutaAbsoluta on Tomato plants. Journal of the Nigerian Society for Mathematical Biology. 2(1): 14-31.
Smith, J., Johnson, A.B., & Lee, C. (2023), "Modeling the coinfection dynamics of hepatitis C and COVID-19: A systematic review," Journal of Epidemiology and Infection, 151(7), pp. 1350–1365.
Udoka B. O., Nometa I. and Bolarinwa B. (2023), Analysis of a model to control the codynamics of Chlamydia and Gonorrhea using Caputo fractional derivative. Mathematical Modelling and Numerical Simulation with Applications, 2023, 3(2), 111–140. Available online at: https://doi.org/10.53391/mmnsa.1320175 - Scopus indexed Journal.
Ullah, A.Z., T. Abdeljawad, Z. Hammouch, K. Shah (2020), "A hybrid method for solving fuzzy Volterra integral equations of separable type kernels," Journal of King Saud University - Science, 33, DOI: https://doi.org/10.1016/j.jksus.2020.101246.
Yunus A.O, M.O. Olayiwola, M.A. Omolaye, A.O. Oladapo, A fractional order model of lassa fever disease using the Laplace-Adomian decomposition method, Health Care Anal. 3 (2023) 100167, www.elsevier.com/locate/health. Health care Analytics.
Zhang, R. M. Li, Bilinear residual network method for solving the exactly explicit solutions of nonlinear evolution equations, Nonlinear Dynam. 108 (2022) http://dx.doi.org/10.1007/s11071-022-07207-x.
Zhang R.F., Li M.-C., J.Y. Gan, Q. Li, Z.-Z. Lan, Novel trial functions and rogue waves of generalized breaking soliton equation via bilinear neural network method, Chaos Solitons Fractals 154 (C) (2022).
Downloads
Published
Issue
Section
License
Copyright (c) 2026 Journal of Science Research and Reviews

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
- Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- NonCommercial — You may not use the material for commercial purposes.
- No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits.




