Numerical Solution of Fractional order Hepatitis B Model Via the Generalized Fractional Adams-Bashforth-Moulton Approach

Abstract

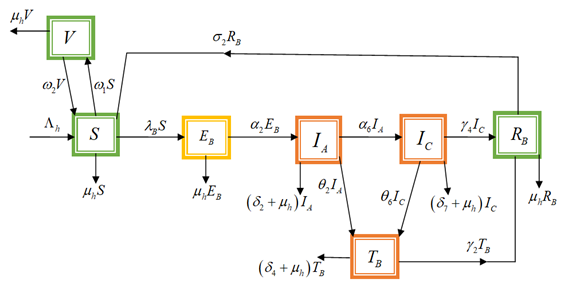
In this paper we examine the epidemiological properties of Hepatitis B virus (HBV) infection based on the equation of a fractional-order mathematical model based on the Caputo derivative. The model uses interventions such as treatment and vaccination as control measures to examine the effect that they have on disease dynamics. We define the presence and uniqueness of solutions in the framework of the fractional order and test the stability of the endemic equilibrium point based on the theory of Lyapunov functions. The model is numerically solved with the help of the fractional Adams-Bashforth-Moulton method to indicate changes in the model parameters and their respective fractional orders into how each one of the above parameters affects the progress of the disease. The use of simulation shows that higher treatment and vaccination rates decreases the prevalence of Hepatitis B and shows the high level of flexibility and realism of the fractional-order models in contrast to the classical integer order equations. In the paper, the importance of fractional modeling in the representation of the effects of memory and nonlocal interaction among the biological systems is highlighted, which enhances the understanding and control of infectious diseases. The model however assumes that the population is homogeneous mixed, and hypothetical values of the parameters thus restrains empirical validation. To make the model more predictive and relevant in practical use in formulating effective control measures on Hepatitis B, future studies need to include spatial heterogeneity, stochastic effects.