Numerical Solution of Fractional Order Chlamydia Model Via the Generalized Fractional Adams-Bashforth-Moulton Approach

Ibrahim Abdulrazaq Abubakar; David Omale; Jeremiah Amos; William Atokolo; Emmanuel Abah; Joseph Achonu Omale; Samson Ojima Makolo; Samuel Kehinde Olayemi; Bolarinwa Bolaji

doi:10.70882/josrar.2025.v2i5.118

Authors

Ibrahim Abdulrazaq Abubakar
Prince Abubakar Audu University, Anyigba
David Omale
Prince Abubakar Audu University, Anyigba
Jeremiah Amos
Prince Abubakar Audu University, Anyigba
William Atokolo
williamsatokolo@gmail.com

Prince Abubakar Audu University, Anyigba
Emmanuel Abah
Prince Abubakar Audu University, Anyigba
Joseph Achonu Omale
Prince Abubakar Audu University, Anyigba
Samson Ojima Makolo
Prince Abubakar Audu University, Anyigba
Samuel Kehinde Olayemi
Prince Abubakar Audu University, Anyigba
Bolarinwa Bolaji
Prince Abubakar Audu University, Anyigba

Keywords:

Chlamydia, Fractional, Adam-Bashforth-Moulton, Transmission, Control, Strategies

Abstract

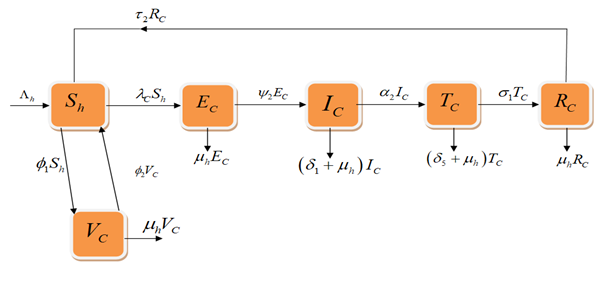
In the present paper we offer the epidemiological parameters of the Chlamydia infection and discuss its dynamics with the help of a fractional-order mathematical model and estimating the role of contact and vaccination rates in the development of interaction with this disease. The conditions of existence and uniqueness of solutions of the problem in the environment of a fractional order were determined. Numerical simulations are carried out to show how the model parameters and fractional-order influence the disease control and their propagation property through the use of the fractional Adams-Bashforth-Moulton method. Additional simulations show that a rise in contact rates and a subsequent reduction of the efficacy of vaccination are the involved factors that contribute to the increase of the prevalence of the Chlamydia. The findings indicate that a preventive strategy to reduce transmission of the infection is a verified method of valuing the low level of the infection transmission over the population

Dimensions

REFERENCES

Abah E., Bolaji B., Atokolo W., Amos J., Acheneje G.O., Omede B.I, Amos J.,Omeje D. (2024), Fractional mathematical model for the Transmission Dynamics and control of Diphtheria ,International Journal of mathematical Analysis and Modelling,Vol.7,ISSN:2682-5694.

Ahmed I., . Goufo E. F. D,Yusuf A., Kumam .P., Chaipanya P., and Nonlaopon K. ( 2021), “An epidemic prediction from analysis of a combined HIV-COVID-19 co-infection model via ABC fractional operator,” Alexandria Engineering Journal, vol. 60, no. 3, pp. 2979–2995.

Ali.Z., Zada.A.,Shah. K., Existence and stability analysis of three-point boundary value problem, Int. J. Appl. Comput. Math.3 (2017) 651–664, http://dx.doi. org/10.1007/s40819-017-0375-8. Milici C., G. Draganescu, J.T. Machado, Introduction to Fractional Differential Equations, Springer, 2018.

Amos J., Omale D., Atokolo W., Abah E., Omede B.I., Acheneje G.O., Bolaji B. (2024), Fractional mathematical model for the Transmission Dynamics and control of Hepatitis C, FUDMA Journal of Sciences, Vol.8,No.5,pp.451-463, DOI: https://doi.org/10.33003/fjs-2024-0805-2883.

Atokolo .W., Omale .D Acheneje .G.O, Paul R.V, Amos .J. (2024) Numerical Analysis of new COVID-19 control model incorporating three Different Fractional operators, Journal of Nonlinear Modelling and Analysis.

Atokolo W a, Remigius .A.O. , Omale .D., Paul .R. V. ,Amos . J., Ocha S. O., (2023) Mathematical modeling of the spread of vector borne diseases with influence of vertical transmission and preventive strategies FUDMA Journal of sciences: Vol. 7 No. 6, December (Special Issue), pp 75 -91 DOI: https://doi.org/10.33003/fjs-2023-0706-2174

Atokolo W a, RemigiusAja .O. ,Omale .D., Ahman .Q. O.,Acheneje G. O., Amos . J. (2024) Fractional mathematical model for the transmission dynamics and control of Lassa fever Journal of journal homepage: www.elsevier. 2773-1863/© 2024com/locate/fraopehttps:// doi.org/10.1016/j.fraope.2024.100110.

Atokolo, W., Aja, R. O., Aniaku, S. E., Onah, I. S., &Mbah, G. C. (2022). Approximate solution of the fractional order sterile insect technology model via the Laplace– Adomian Decomposition Method for the spread of Zika virus disease.International Journal of Mathematics and Mathematical Sciences, (1), 2297630.

Baskonus. H.M., Bulut H., (2015) On the numerical solutions of some fractional ordinary differential equations by fractional Adams Bashforth-Moulton Method, Open Math. 13 1.

Bonyah. E., Zarin, R. Fatmawati, Mathematical modeling of Cancer and Hepatitis co-dynamics with non-local and nonsingular kernal, 2020, 2052–2541.https://doi.org/10.28919/ cmbn/5029.

Chlamydia – CDC basic fact sheet [Internet]. USA: CDC; Available from: https://www.cdc.gov/std/chlamydia/stdfact-chlamydia.htm

Das, R., Patel, S., & Kumar, A. (2024), "Mathematical modeling of hepatitis C and COVID-19 coinfection in low- and middle-income countries: challenges and opportunities,"BMC Public Health, 24(1), pp. 587.

Diethelm .K., (2022) The Frac PECE subroutine for the numerical solution of differential equations of fractional order,.DOI: https://doi.org/10.33003/fjs-2023-0706-2174.

Emmanuel. L. M., Omale .D., Atokolo .W., Amos .J., Abah .E., Ojonimi.A.A, Onoja T, Acheneje .G.O, Bolaji B.(2025), Fractional mathematical model for the dynamics of pneumonia transmission with control using fixed point theory. GPH-International Journal of Mathematics, 8(5), 01-31.

Jalija E., Amos J, Atokolo .W., Omale .D., Abah .E., Alih .U., Bolaji .B. (2025), Numerical investigations on Dengue fever model through singular and non-singular fractional operators. International Journal of Mathematical Analysis and Modelling.

Jalija E., Amos J., Benjamin A., Bolarinwa .B., (2025), fractional order model for HIV/AIDS:Analytical and Generalized fractional Adams-Bashforth-Moulton Approach. Journal of management and Technology.

Joseph.E., Lebechi .F. A., Atokolo W, Amos .J., (2025), Numerical solution of fractional order Chlamydia model via the generalized Fractional Adams-Bashforth-Moulton Approach. International Journal of mathematics.

Newman L, Rowley J, Vander Hoorn S, Wijesooriya NS, Unemo M, Low N, et al.( 2015) Global estimates of the prevalence and incidence of four curable sexually transmitted infections in 2012 based on systematic review and global reporting. PLoS One.;10:e0143304.

Nyarko C.C., Nsowa-Nuamah. N. N. N., Nyarko.P. K., Wiah .E. N., Buabeng .A. Modelling Chlamydia trachomatis infection among Young women in Ghana: A case study at Tarkwa NsuaemMunicipalityAm. J. Appl. Math., 9 (3) (2021), pp. 75-85.

Odionyenma U.B., Omame A., Ukanwoke N.O., NometaI.Optimal control of Chlamydia model with vaccinationInt. J. Dyn. Control, 10 (1) (2022), pp. 332-348.

Omede.B. I, Israel. M.,Mustapha .M. K. , Amos J. ,Atokolo .W. , and Oguntolu .F. A. (2024) Approximate solution to the fractional soil transmitted Helminth infection model using Laplace Adomian Decomposition Method.Journal of mathematics. (2024) Int. J. Mathematics. 07(04), 16-40.

Paavonen J, Eggert-Kruse W. (1999) Chlamydia trachomatis: impact on human reproduction. Hum Reprod Update.; 5:433–47.

Paavonen J, Lehtinen M. (1996), Chlamydial pelvic inflammatory disease. Hum Reprod Update.; 2:519–29.

Philip J., Omale D., Atokolo W., Amos J., Acheneje G.O., Bolaji B. (2024), Fractional mathematical model for the Transmission Dynamics and control of HIV/AIDs,FUDMA Journal of Sciences,Vol.8,No.6,pp.451-463, DOI: https://doi.org/10.33003/fjs-2024-0805-2883.

Podlubny.I., (1998) Fractional differential equations, an introduction to fractional derivatives, in:Fractional Differential Equations, to Methods of their Solutions and Some of their Applications, Elsevier.

Samanta G.P., Sharma.S., Analysis of a delayed Chlamydia epidemic model with pulse vaccination Appl. Math. Comput., 230 (2014), pp. 555-569.

Sharma.S., Samanta .G.P. Analysis of a Chlamydia epidemic model J. Biol. Syst., 22 (04) (2014), pp. 713-744.

Smith, J., Johnson, A.B., & Lee, C. (2023), "Modeling the coinfection dynamics of hepatitis C and COVID-19: A systematic review,"Journal of Epidemiology and Infection, 151(7), pp. 1350–1365.

Thylefors B, Négrel AD (1995), Pararajasegaram R, Dadzie KY. Global data on blindness. Bull World Health Organ. 73:115–21.

Ullah. A.Z. T. Abdeljawad, Z. Hammouch, K. Shah, A hybrid method for solving fuzzy Volterra integral equations of separable type kernels, J. King Saud Univ. - Sci. 33 (2020) http://dx.doi.org/10.1016/j.jksus.2020.101246.

World Health Organization (2021) Sexually transmitted infections Available from: https://www.who.int/en/news-room/fact-sheets/detail/sexuallytransmittedinfections-(stis)

World Health Organization (2022) Global prevalence and incidence of selected curable sexually transmitted infections: overview and estimates [Internet]. c2001. Available from: https:// apps.who.int/iris/bitstream/handle/10665/66818/?sequence=1.

World Health Organization. (2021) Global progress report on HIV, viral hepatitis and sexually transmitted infections, 2021: accountability for the global health sector strategies 2016–2021: actions for impact: web annex 2: data methods. World Health Organization.

Yunus. A.O, M.O. Olayiwola, M.A. Omolaye, A.O. Oladapo, (2023) A fractional order model of lassa fever disease using the Laplace-Adomian decomposition method, Health Care Anal. 3 100167, www.elsevier.com/locate/health.Health care Analytics.

Zhang.R.F.,Li. M.-C.,Gan. J.Y., Li.Q., Lan.Z.-Z., (2022). Novel trial functions and rogue waves of generalized breaking soliton equation via bilinear neural network method, Chaos Solitons Fractals 154 (C). Results in Physics, vol. 37, article 105498.